Matplotlib
丹丹
 2019-06-24 00:00:00    935 Words  5 Mins  

基本配置与标记

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#coding:utf-8

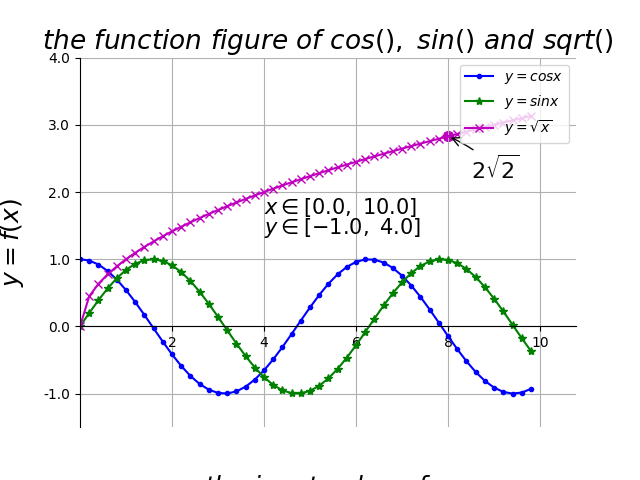
import numpy as np
import matplotlib.pyplot as plt
from pylab import *

# 定义数据部分
x = np.arange(0., 10, 0.2)
y1 = np.cos(x)
y2 = np.sin(x)
y3 = np.sqrt(x)

# 绘制 3 条函数曲线
plt.plot(x, y1, color='blue', linewidth=1.5, linestyle='-', marker='.', label=r'$y = cos{x}$')
plt.plot(x, y2, color='green', linewidth=1.5, linestyle='-', marker='*', label=r'$y = sin{x}$')
plt.plot(x, y3, color='m', linewidth=1.5, linestyle='-', marker='x', label=r'$y = \sqrt{x}$')

# 坐标轴上移
ax = plt.subplot(111)
ax.spines['right'].set_color('none')     # 去掉右边的边框线
ax.spines['top'].set_color('none')       # 去掉上边的边框线

# 移动下边边框线，相当于移动 X 轴
ax.xaxis.set_ticks_position('bottom')    
ax.spines['bottom'].set_position(('data', 0))

# 移动左边边框线，相当于移动 y 轴
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))

# 设置 x, y 轴的取值范围
plt.xlim(x.min()*1.1, x.max()*1.1)
plt.ylim(-1.5, 4.0)

# 设置 x, y 轴的刻度值
plt.xticks([2, 4, 6, 8, 10], [r'2', r'4', r'6', r'8', r'10'])
plt.yticks([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], 
    [r'-1.0', r'0.0', r'1.0', r'2.0', r'3.0', r'4.0'])

# 添加文字
plt.text(4, 1.68, r'$x \in [0.0, \ 10.0]$', color='k', fontsize=15)
plt.text(4, 1.38, r'$y \in [-1.0, \ 4.0]$', color='k', fontsize=15)

# 特殊点添加注解
plt.scatter([8,],[np.sqrt(8),], 50, color ='m')  # 使用散点图放大当前点
plt.annotate(r'$2\sqrt{2}$', xy=(8, np.sqrt(8)), xytext=(8.5, 2.2), fontsize=16, color='#090909', arrowprops=dict(arrowstyle='->', connectionstyle='arc3, rad=0.1', color='#090909'))

# 设置标题、x轴、y轴
plt.title(r'$the \ function \ figure \ of \ cos(), \ sin() \ and \ sqrt()$', fontsize=19)
plt.xlabel(r'$the \ input \ value \ of \ x$', fontsize=18, labelpad=88.8)
plt.ylabel(r'$y = f(x)$', fontsize=18, labelpad=12.5)

# 设置图例及位置
plt.legend(loc='upper right')    
# plt.legend(['cos(x)', 'sin(x)', 'sqrt(x)'], loc='up right')

# 显示网格线
plt.grid(True)    

# 绘图
plt.savefig("../img/2019-06-24_Matplotlib基本语法_1.png")
plt.close()

曲线图

1
2
3
4
5
6
7
x = np.arange(-5,5,0.1)
y = x ** 2
plt.plot(x,y)

# 绘图
plt.savefig("../img/2019-06-24_Matplotlib基本语法_2.png")
plt.close()

散布图

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt

n = 1024
X = np.random.normal(0, 1, n)
Y = np.random.normal(0, 1, n)

plt.scatter(X,Y)

# 绘图
plt.savefig("../img/2019-06-24_Matplotlib基本语法_3.png")
plt.close()

柱状图

1
2
3
4
5
6
x = np.random.normal(size=1000)
plt.hist(x, bins=10)

# 绘图
plt.savefig("../img/2019-06-24_Matplotlib基本语法_4.png")
plt.close()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
import matplotlib.pyplot as plt

n = 12
X = np.arange(n)
Y1 = (1- X / float(n)) * np.random.uniform(0.5, 1.0, n)
Y2 = (1- X/ float(n)) * np.random.uniform(0.5, 1.0, n)

plt.axes([0.025, 0.025, 0.95, 0.95])
plt.bar(X, +Y1, facecolor = '#9999ff', edgecolor = 'white')
plt.bar(X, -Y2, facecolor = '#ff9999', edgecolor = 'white')

for x,y in zip(X,Y1):
    plt.text(x, y + 0.08, '%.2f' % y, ha = 'center', va = 'bottom')

for x,y in zip(X,Y2):
    plt.text(x, -y - 0.08, '%.2f' % y, ha = 'center', va= 'top')

plt.xlim(-.5, n), 
plt.ylim(-1.25, +1.25), 
plt.xticks([])
plt.yticks([])

# 绘图
plt.savefig("../img/2019-06-24_Matplotlib基本语法_5.png")
plt.close()

3D图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X ** 2 + Y ** 2)
Z = np.sin(R)

ax.plot_surface(X, Y, Z, rstride = 1, cstride=1, cmap = plt.cm.hot)
ax.contourf(X, Y, Z, zdir = 'z', offset = -2, cmap = plt.cm.hot)
ax.set_zlim(-2,2)

# 绘图
plt.savefig("../img/2019-06-24_Matplotlib基本语法_6.png")
plt.close()

参考：

  1. 廖雪峰Python数据分析