线性回归
丹丹
 2019-07-14 00:00:00    630 Words  3 Mins  

创建数据

1
2
3
4
5
6
def make_data(nDim):
    x0 = np.linspace(1, np.pi, 50)
    x = np.vstack([[x0,], [i**x0 for i in range(2, nDim+1)]])
    y = np.sin(x0) + np.random.normal(0,0.15,len(x0))
    
    return x.transpose(), y

最小二乘法 Ordinary Least Squares (OLS)

目标函数：

不足：OLS为了更好的拟合数据，会使用较大的w值，进而导致过度拟合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model

dims = [2, 6, 12, 24]
plt.figure(figsize=(10, 10))

for idx, i in enumerate(dims):
    
    plt.subplot(2, 2, idx+1)
    x, y = make_data(i)

    reg = linear_model.LinearRegression()
    reg.fit(x, y)

#     reg.intercept_
#     reg.coef_

    plt.scatter(x[:, 0], y, marker = '*', color = 'r', label = 'samples')
    plt.plot(x[:, 0], [reg.predict([x[i, :]]) for i in range(len(y))], linestyle = '--', label = 'model')
    plt.legend(loc='upper right')
    plt.title('Dimensions: %s' %i, fontsize=19)

plt.savefig("../img/2019-07-14_线性回归_1.png")
plt.close()

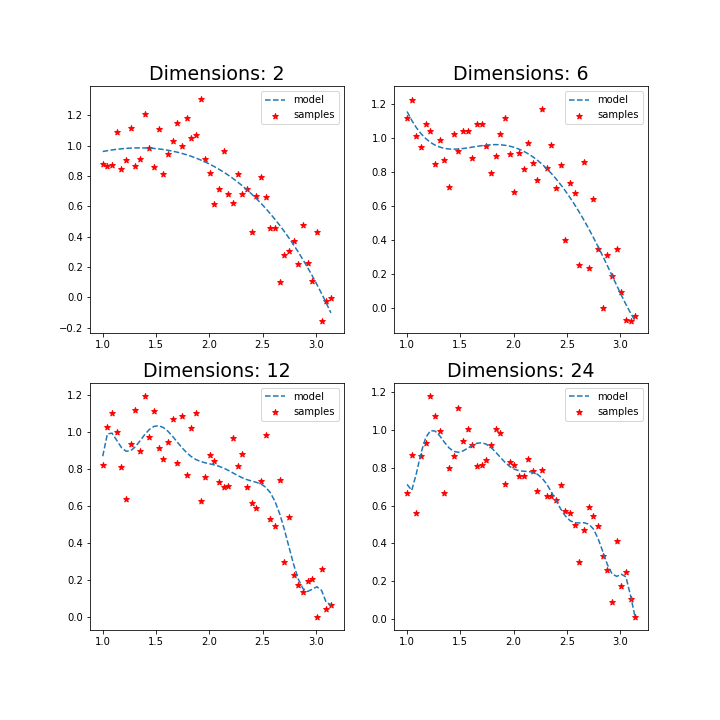
岭回归 Ridge Regression (Tikhonov Regularization)

目标函数：

优化：为惩罚OLS每个w逐渐增加导致过度拟合的问题，新增的项为L2惩罚项(L2 Penalty)。
特点：w有可能特别小的绝对值，但很难达成0，造成贡献很小的系数还是要放，影响性能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model

dims = [2, 6, 12, 24]
plt.figure(figsize=(10, 10))

for idx, i in enumerate(dims):
    
    plt.subplot(2, 2, idx+1)
    x, y = make_data(i)

    reg = linear_model.Ridge(alpha = 100)
    reg.fit(x, y)

#     reg.intercept_
#     reg.coef_

    plt.scatter(x[:, 0], y, marker = '*', color = 'r', label = 'samples')
    plt.plot(x[:, 0], [reg.predict([x[i, :]]) for i in range(len(y))], linestyle = '--', label = 'model')
    plt.legend(loc='upper right')
    plt.title('Dimensions: %s' %i, fontsize=19)
    
plt.savefig("../img/2019-07-14_线性回归_2.png")
plt.close()

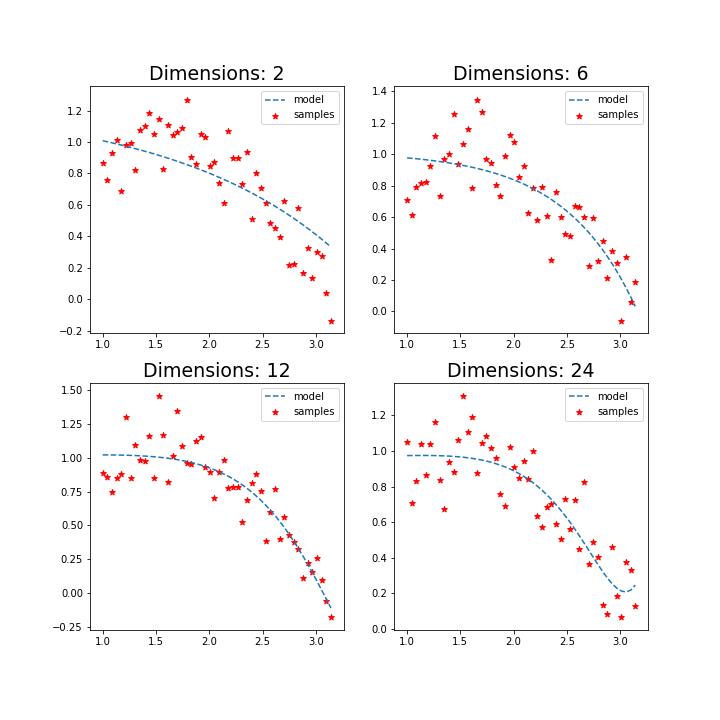
Lasso 回归

目标函数：

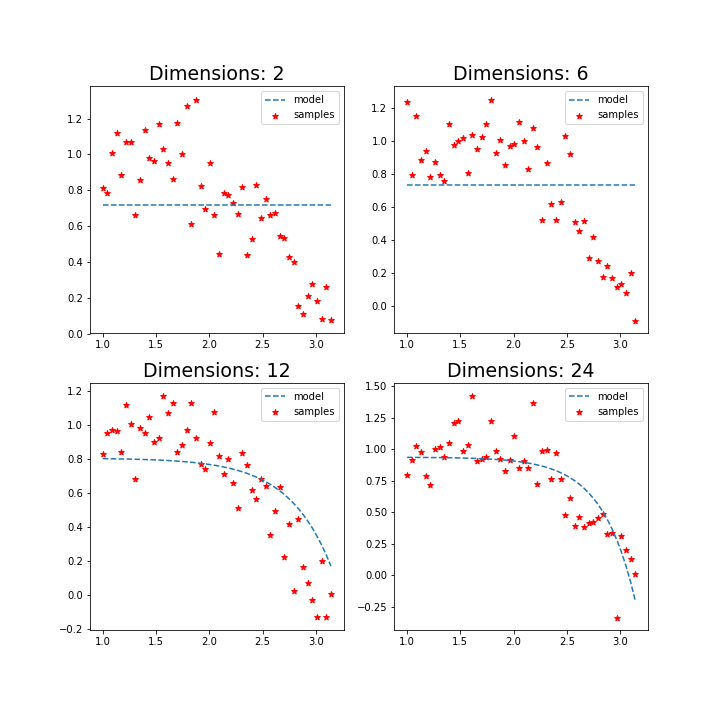
优化：为惩罚OLS每个w逐渐增加导致过度拟合的问题，新增的项为L1惩罚项(L1 Penalty)。
特点：比L2惩罚项严厉很多，可以产生稀疏回归参数，即多数回归参数为零。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model

dims = [2, 6, 12, 24]
plt.figure(figsize=(10, 10))

for idx, i in enumerate(dims):
    
    plt.subplot(2, 2, idx+1)
    x, y = make_data(i)

    reg = linear_model.Lasso(alpha = 100)
    reg.fit(x, y)

#     reg.intercept_
#     reg.coef_

    plt.scatter(x[:, 0], y, marker = '*', color = 'r', label = 'samples')
    plt.plot(x[:, 0], [reg.predict([x[i, :]]) for i in range(len(y))], linestyle = '--', label = 'model')
    plt.legend(loc='upper right')
    plt.title('Dimensions: %s' %i, fontsize=19)

plt.savefig("../img/2019-07-14_线性回归_3.png")
plt.close()

参考：

  1. 从机器学习到深度学习：基于Scikit-learn与TensorFlow的高效开发实战